Suite des articles visant à améliorer l’illumination de la scène, après une couleur diffuse correctement éclairée grâce aux normales et aux spéculaires, il restait, invariablement, que l’image entière était éclairée uniformément concernant l’intensité, pour une même direction de normales.
Les calculs et les informations transmises étaient insuffisantes pour calculer la valeur de chaque pixel et, surtout, rien ne nous permet de savoir où le pixel se situe dans l’espace, nous permettant de faire varier son illumination sur base d’une distance altérée par sa position.
Je ne suis pas 3D
N’oubliez pas que ce que vous voyez n’est pas de la 3D, mais une succession d’images plates représentant « un quelque chose » en 3D, et c’est cet enchevêtrement savamment orchestré qui vous dit que l’image est 3D. Tout n’est qu’illusion Mr. Anderson ! Et votre cerveau vous trompe, et c’est le but !
Je l’ai déjà dit dans les précédents articles, mais c’est là tout le problème, comment donner une information 3D à une image plate ? Certes nous avons les normales pour nous donner la direction, mais qu’en est-il de la position ? Comment puis-je savoir que le haut de mon bloc est une surface au Z équivalant, variant sur X et Y ?
Reprenons depuis le Zébut
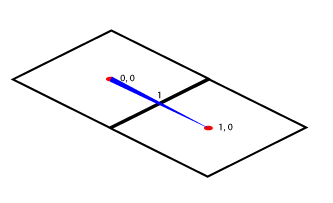
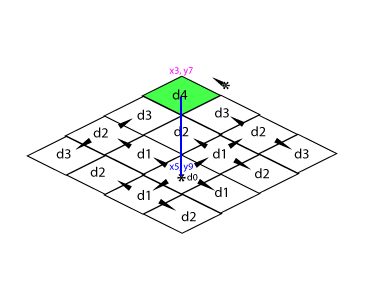
Un Tile est l’image représentant une zone, une unité de notre grille. Celle-ci a ses coordonnées X et Y. La distance entre leur position sera de 1 (1x, 1y ou 1x1y).
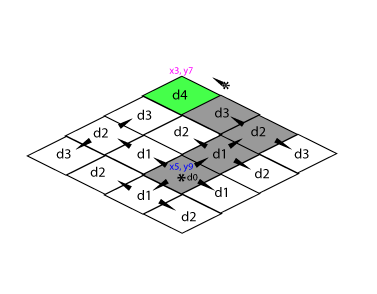
L’éclairage d’un Tile est soumis à la propagation de la lumière dans le subset de la map courante (cela nous rappelle de vieux souvenir [2018 !]). La propagation reste importante pour savoir quel Tile est impliqué dans l’éclairage (optimisation).
On parlera donc de la distance (parcourue ici) entre le Tile que l’on veut éclairer par rapport à la source lumineuse et sa force.
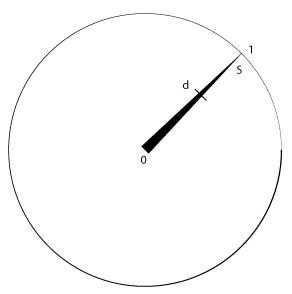
Une lumière peut donc éclairer sur une distance (d) un objet proportionnellement à sa force (S) à cette distance et selon l’intensité (i) de cette lumière. Nous obtenons alors le facteur (f) d’éclairage du pixel (rgb aux coordonnées uv).
f = (1 - (d * (1 / S))) * iOn obtient une valeur (float) allant de 0 à 1, qui sera notre facteur d’éclairage du Tile.
Ça c’était avant
Ce qu’il nous manquait jusque là c’est d’avoir toutes les coordonnées au niveau du shader pour effectuer ce calcul de distance au niveau du pixel.
On calculera ainsi notre distance autrement, c’est-a-dire sur base des coordonnées du Tile (t) et de la lumière (l), sans oublie l’intensité (i).
d = √((l.x - t.x)² + (l.y - t.y)²) * iDonc on propage, on définit pour chaque Tile concernés les lumières impliquées, on ajoute les informations manquantes jusqu’alors et … ? Ben jusque là rien de nouveau sauf une distance plus correspondante à l’origine mais pas par rapport aux obstacles rencontrés entre la source et l’élément éclairé, car ça, je suis sur que vous les aviez oubliés.
On ne traverse pas un mur, la lumière « contourne » par rebond etc. Donc la propagation reste la bonne manière mais ne donnera pas le bon résultat en isométrique, et j’espère que vous comprenez pourquoi avec toute cette suite d’articles ahah. En bref, on a pas la possibilité de savoir comment la lumière est arrivée à chaque pixel, il faudrait calculer pour chaque objet un pixel de rebond (surement sa normale), balayer ainsi dans tous les sens et à chaque contact : éclairer ce pixel et modifier le rayon pour le faire repartir (couleur, angle, puissance, …), bref on réinventerai un rendu par projection de rayons en 2D sur base d’information 3D stockée dans les textures. Non !
Spatiale 3D dans de la 2D
Ce qu’il nous manque à cette étape est le moyen de faire évoluer notre formule de calcul de la distance pour inclure la position du pixel rendu de notre texture.
Nous avions vu plus haut que le Tile se définit par une position X et Y, ici en sont centre, sur la partie supérieur pour représenter le sol. Nous ne parlerons pas de Z ici mais l’idée sera la même une fois que j’aurais réussi à ramener l’information jusqu’au shader.
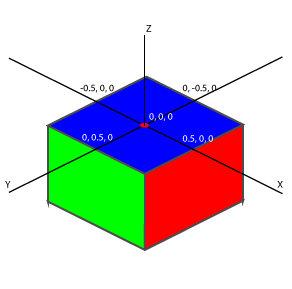
Si un Tile est à une distance de 1 de ses voisins alors il a à ses extrémités un delta variable de [-0.5, 0.5] en X et en Y. Z étant, lui, soumis à un facteur d’élévation définit par la scène, ici de 8 pixels, et donc aura une idée différente de sa distance, du moins c’est ainsi que l’élévation avait été définie au tout début.
Nous avions jusque là 3 textures : la diffuse (l’image elle-même), la normale (direction d’éclairage) et le spéculaire (carte de où appliquer le spéculaire). Et bien nous allons en ajouter une nouvelle.
Suivant la même idée que pour la texture de normales, nous réutiliserons notre définition RGB de nos repères : X en rouge, Y en vert et Z en bleu. Pour chaque pixel de l’image nous définirons ainsi sa position relative par une valeur RGB. Ne pas oublier que le centre ne sera pas 0, car nous avons besoin des deltas négatif, ainsi nous commencerons au centre à 128,128,128.
Un programme, un plugin, ou une théorie pour le faire de manière automatique n’existant pas, on va devoir y mettre de l’huile de coude.


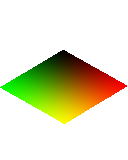

Ainsi comme vous pouvez le voir, si on veut s’aider, nous pourrons compter sur les gradient, un bon dégradé bien réfléchi qui sera combiné à une couche supplémentaire. Nous commencerons par le XY et on surcouchera par le Z. Un total de 2h nécessaire avant d’arriver au résultat que voici.

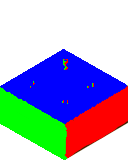

Notre formule de distance peut donc être complétée par cette nouvelle information (pp).
d = √((l.x - (t.x + pp.x))² + (l.y - (t.y + pp.y))²) * iCe qui nous donnera sans plus attendre ce premier résultat :
Wow que se passe-t-il ? On a notre dégradé * fête * cependant nous avons un drôle d’aspect sur certain Tile. Notre algo utilise la force (S) pour se propager, mais comme vous l’avez vu, la propagation est plus courte que le segment calculable en ligne droite donc nous arrivons trop court, nous n’avons pas assez s’électionné de Tiles pour notre impact. L’idée serait surement de refaire un calcul sur base de la distance au lieu de calculer le nombre de saut, mais pour le workaround j’ai ajouté +2 à la force (S).
On en profite pour restaurer le calcul du spéculaire maintenant que nous avons de vraies informations et ce foutu éclair blanc au coffre s’en va !
Il y a bien évidemment des effets de bords, comme le fait que la distance parcourue n’étant plus impliquée, si vous fermez la porte, le Tile de l’autre côté sera éclairé comme si vous étiez à côté au lieu d’un faible éclairage (la lumière fait le tour du mur). Les tables clignotent et là je ne sais pas encore pourquoi. C’est plus joli mais moins cohérent. On en revient à l’idée des rebonds, du vecteur qui doit bouger selon l’idée mais rendre chaque Tile cohérent entre eux, là je ne vois pas comment.
J’ai quand même regardé comment ajouter la distance à la formule mais le résultat empirique n’est pas terrible.
Et en fait si on déplace la lumière selon la distance parcourue dans la même direction, on éloigne alors virtuellement notre Tile voisin. Et ainsi le résultat tiens compte de la distance. Ceci dit l’éclairage en a pris un coup, il y a surement quelque chose à faire avec ça.
lightPos += lightDirection * lights[i].distance;Pour bien faire il faudra savoir si la distance correspond à un voisin, et ainsi différencier si notre voisin a une distance de 4 ou de 1 et appliquer l’éloignement que dans ce cas. Reste à trouver comment faire.
Et ensuite ?
Comme toujours, quelle est l’étape suivante et comment adresser les nouveaux problèmes, ou ceux mis de côté ? Plus j’avance dans TARS et plus les limites, personnelles et techniques se montrent. Il est grisant de se dire que j’ai relevé un défi qui, selon Google, n’a pas été adressé ou n’est actuellement plus référencé. Il faut aussi se rendre compte de l’effort considérable que cela demanderait si l’on voulait faire un jeu entier ainsi. Et là encore nous n’avons exploré que la lumière (par rapport à l’existant réalisé).
C’est le cœur serré que je me dis que j’ai clôturé cette étape, et qu’il faut, car le temps n’est pas infini, et que je n’ai pas que ce projet à faire, passer à autre chose… Quand je dis « passer à autre chose« , ce n’est certainement pas abandonner Nahyan, certes non ! Mais explorer (enfin) une autre piste que celle de tout faire moi-même, même si je n’ai pas fort le choix. Je ne vais pas en dire plus pour le moment, j’ai déjà commencé à explorer d’autres possibilités et vous raconterais le moment venu.
Cela fait 7 ans que TARS existe, avec une belle pause au milieu, et 2-3 belles phases de développement, comme le passage au WebGL pour adresser les performances sur l’éclairage première version, ou encore la refonte des classes communes pour mieux gérer les données et factoriser le code générique. Et enfin ici, le nouveau système d’éclairage, mais in fine rien de plus, nous n’avons toujours pas vu « Le temple du Prisme« , un HéroQuest ou un Liebesstein.
Qui sait que j’y toucherai par défi encore 😉